• Scope: 1 month
• Keywords: Electric Vehicle, Microgrid, Charging Station, Optimization, MILP, Software Development
• Tools: Python, Pyomo, CBC Solver
• Other Contributors: P. Losi, O. Olugbayila, Y. Li
• Links: [Github] [PDF]

The Problem

In this project, my team and I intend to devise a strategy for charging a pool of electric vehicles in an industrial-like microgrid. The electricity used in the microgrid can come from a main grid or from PV panels or from both. Additionally, there is a limit on the power that can be imported from or exported to the grid. The challenge is to minimize a trade-off between the costs of the electricity purchased to operate the charging station and the penalty incurred to the EV owners if their desired state of charge at departure time is not met.

Requirements

It is assumed that every EV has access to a charging station when it arrives at the parking. Each hour, the controller also receives a forecast of arrivals and of PV power generation for the current day. If technically possible, all the EVs must receive some power (i.e, the price the EVs are willing to pay is higher than the grid import price) but the desired departure state of charge should not be exceeded.

Furthermore, the charging strategy should allocate power among EVs using a priority index that tends to favor EVs that will stay longer periods of time and have little capacity, unless the EV owner is ready to pay more for a fast charge.

• An uncertain arrival and departure time
• An arrival and desired departure state of charge (SOC)
• A battery capacity
• A maximum charging power and a charging efficiency function of the charge power
• The price the owner is willing to pay for the energy charged

Implementation

To design the charging station's controller, we model the problem as a MILP optimization with constraints. Here is an overview of the steps taken to solve the optimization problem.

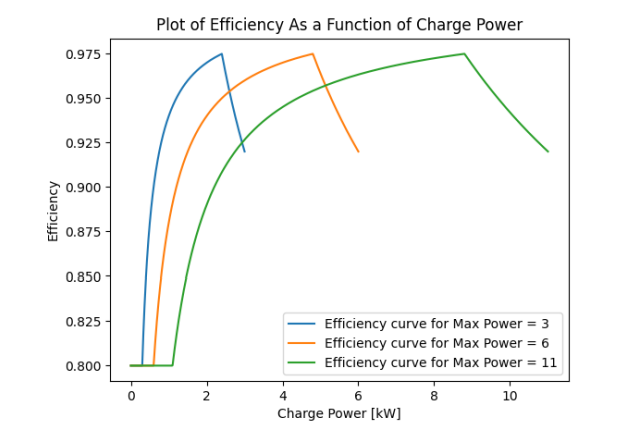
Defining Efficieny as a Function of Charge Power

Given the variation of the state of charge of an EV per unit time as a function of the charge power, we determine the piecewise expression of charge efficiency as a function of the charge power The figure below shows the efficiency curves for three different values of maximum charging power (3, 6, 11 kW) used in the case study validating the controller. The first part of the plot presents a linear variation whereas the second and third sections are clearly nonlinear.

Defining the Model and its Constraints

We mathematically model an objective function to minimize cost of electricity imports from the grid, with consideration to the penalty owed to EV owners if their desired state of charge is not met and with the willingness to maximize revenue from selling unused PV power to the main grid. In addition, we included a trade-off coefficient "alpha" accounting for the system designer’s priority toward minimizing import costs, prioritizing charging the EVs or balancing the two possibilities.

And the described objective function is subjected to the following constraints:

• Energy Equilibrium Constraint: Energy imports from the grid and PV generation must equal Energy used to charge the EVs plus Exports to the grid (if any)
• PV Power Constraint: Balance between Forecast values of PV generation and the actual usage from the PV panels to charge the EVs is taken into account. Any spill overs are exported to the Grid
• Avoid Energy Import & Export Simultaneously
• Penalty incurred to EV owners: This constraint is added to ensure that customer’s satisfaction is considered whilst trying to minimize overall cost of imports from grid
• Maximum Power transfer to EVs: At every timestep, the limit of power that can be transferred to the EVs is less or equal to its Maximum charging power

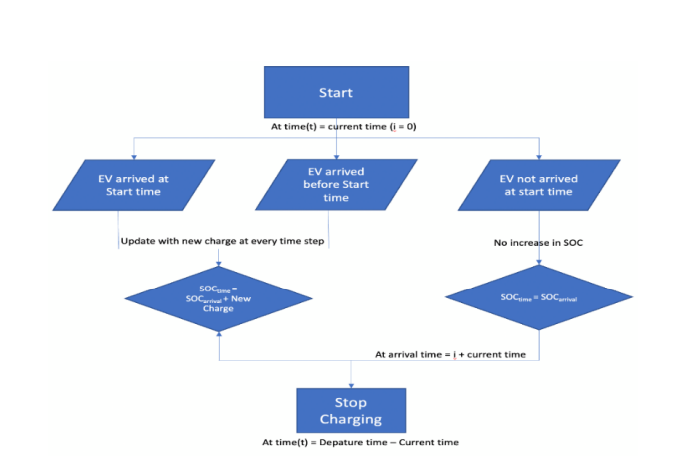
Charging Operation Strategy

The following charging operation strategy allows us to dictate how the state of charge of the EVs is updated with respect to our knowledge of the different possible states (“Connected”, “gone” or “not yet arrived”) and with respect to each time step of the simulation.

Results

We create a scenario with 3 EVs and the following input features for each EV

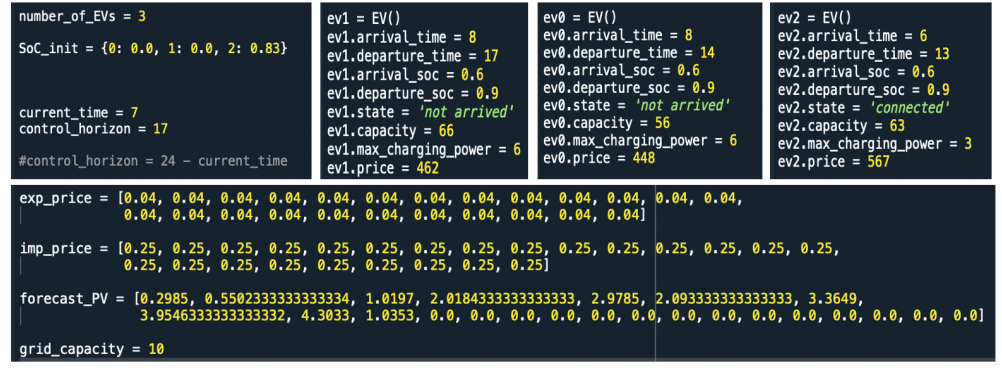
Simulation was performed with a timestep of 1hour and changing values of the previously mentioned tradeoff coefficient "alpha".
The following figure depicts the variation of import costs, export revenue and cost due to penalty with regard to "alpha".

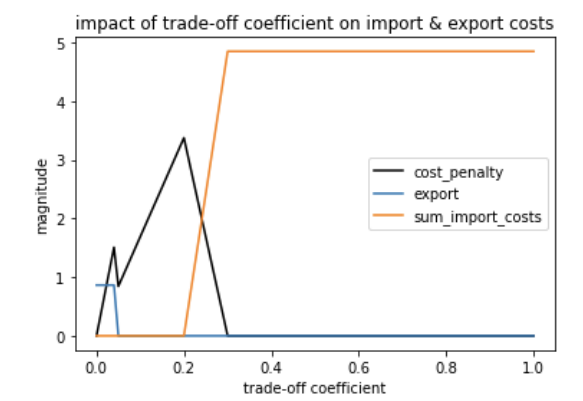
• Alpha between 0 and 0.04(= export price): with the this low value of the coefficient, there is no penalties for not charging the EVs; therefore, the model prioritizes revenue from exports to the grid in order to minimize the objective function
• Alpha between 0.05 and 0.3: there is no incentive to import power from the grid to satisfy the customer’s EVs to their desired state of charge, as the model can still minimize overall cost, just from PV exports to the grid with little penalty costs to be paid.
• Alpha larger than 0.3: at this value of trade-coefficient, the model prioritizes reducing the penalty costs because satisfying the customers by matching their desired SOC with the Departure SOC will lead to overall cost reduction, at least when compared to exports at that value of alpha .

Power Flow Results in the charging center at each time step for alpha = 0.7

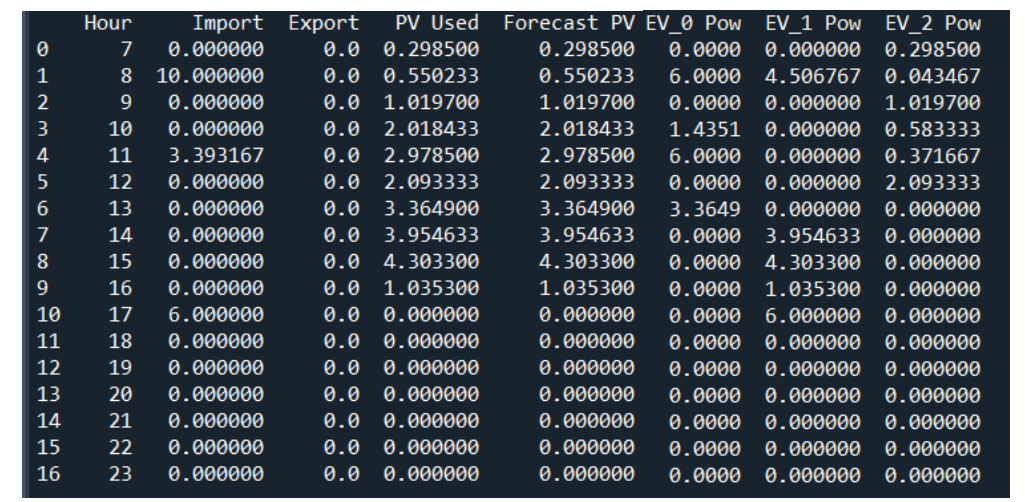
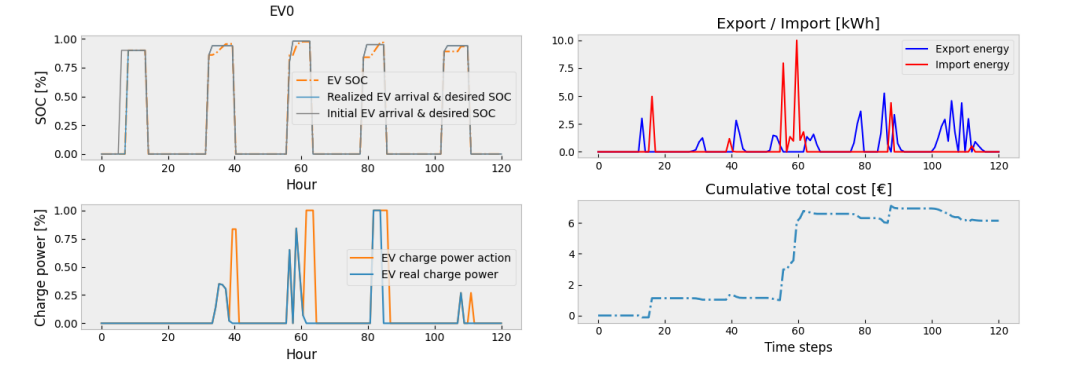
By implementing the optimization problem as detailed above, we have continuously adjusted the value of the trade-off coefficient coefficient from 0 up to 500, value at which we have obtained an accuracy of 98.48% (best accuracy among 10+ teams) when called upon by a desiganted simulator. The following figure displays the performance of our controller in terms of allocating values of EV SOC close enough to the desired SOC. One can also see a comparison between our realized charge power distribution and the EV real charge power.